コンテキストベクトル

あるトークン $i$ に対応するコンテキストベクトル $\mathbf{c}_i$ とは,\[\mathbf{c}_i = \sum_{j=1}^{n} \alpha_{ij} \mathbf{v}_j\].

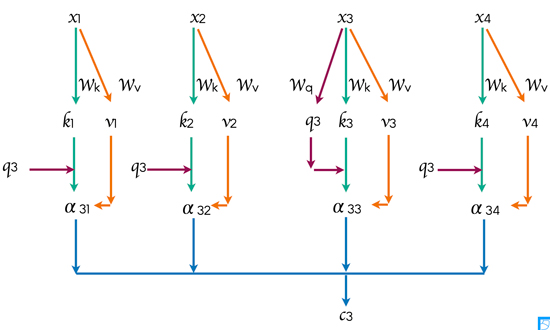
但し,重み係数 $\alpha_{ij}$ は, Query ベクトル $\mathbf{q}_i$ と Key ベクトル $\mathbf{k}_j$ のスケーリング付き内積に対してソフトマックス関数を適用することで定義される.\[\alpha_{ij} = \frac{\exp\left( \frac{\mathbf{q}_i^\top \mathbf{k}_j}{\sqrt{d}} \right)}{\sum_{l=1}^{n} \exp\left( \frac{\mathbf{q}_i^\top \mathbf{k}_l}{\sqrt{d}} \right)}\]

ここで,

• $\mathbf{q}_i \in \mathbb{R}^d$ はトークン $i$ の Query ベクトル
• $\mathbf{k}_j \in \mathbb{R}^d$ はトークン $j$ の Key ベクトル
• $\mathbf{v}_j \in \mathbb{R}^d$ はトークン $j$ の Value ベクトル
• $d$ は各ベクトルの次元数
• $n$ はトークンの総数

すなわち,コンテキストベクトル $\mathbf{c}_i$ は,系列内のすべてのトークン $j$ の Value ベクトルを,Query と Key の相互作用に基づく重み $\alpha_{ij}$ により線形結合したベクトルである.