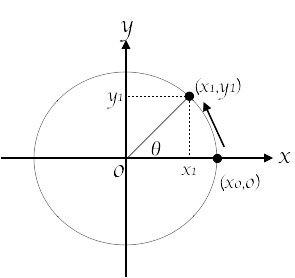
点 $(x_{0},0)$ を $\theta$ だけ反時計回りに回転させて,点 $(x_{1},y_{1})$ に移動させたとき,\[\begin{bmatrix}x_{0}\\0\end{bmatrix}=\begin{bmatrix}1\\0\end{bmatrix}\]であることと,上図の円の半径が $1$ であることから,\[\begin{bmatrix}x_{1}\\y_{1}\end{bmatrix}= \begin{bmatrix}\cos(\theta) \\ \sin(\theta) \end{bmatrix} = \begin{bmatrix}\cos(\theta)& * \\ \sin(\theta)&*\end{bmatrix} \begin{bmatrix}1\\0\end{bmatrix}\]となる.
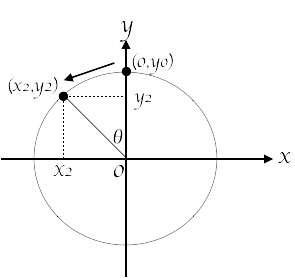
また,点 $(0,y_{0})$ を $\theta$ だけ反時計回りに回転させて,点 $(x_{2},y_{2})$ に移動させたとき,\[\begin{bmatrix}0\\y_{0}\end{bmatrix}=\begin{bmatrix}0\\1\end{bmatrix}\]であることと,上図の円の半径が $1$ であることから,\[\left[ \begin{array}{c}x_{2}\\y_{2}\end{array}\right] =\left[ \begin{array}{c}-\sin(\theta) \\ \cos(\theta) \end{array}\right] =\left[ \begin{array}{cc}* & -\sin(\theta) \\ * & \cos(\theta) \end{array}\right] \left[\begin{array}{c}0\\1\end{array}\right]\]となる.
以上より,2次元回転行列は,\[\begin{bmatrix}\cos(\theta)&-\sin(\theta) \\ \sin(\theta)&\cos(\theta)\end{bmatrix}\]となる.
なお,時計回りに回転させた場合の2次元回転行列は,\[\begin{bmatrix}\cos(-\theta)&-\sin(-\theta) \\ \sin(-\theta)&\cos(-\theta)\end{bmatrix}\]となる.
ここで,\[\cos(-\theta)=\cos(\theta),\sin(-\theta)=-\sin(\theta) \]となることを考慮すると,結局,2次元回転行列は,\[\begin{bmatrix}\cos(\theta)&\sin(\theta) \\ -\sin(\theta)&\cos(\theta)\end{bmatrix}\]となる.
この2次元回転行列は,\[ T(\theta)\]と表される.
これを用いると,点 $\textbf{x}$ を 点 $\textbf{x'}$ に角度 $\theta$ だけ時計回りに回転させる場合は,\[\textbf{x'} =T(\theta) \textbf{x} \]となる.
Mathematics is the language with which God has written the universe.