水平面上で物体が角加速度 $\omega$ ,半径 $r$ の円運動をしているとします.この物体が $T$ 秒掛けて円を一周しているならば,角速度は,\[\omega=\frac{2\pi}{T}[s^{-1}]\]と表せます.$[s^{-1}]$ は単位です.
円周は,$2\pi r$ であるので,この円周を $T$ 秒掛って一周するので,速度 $V$ は \[V=\frac{2\pi r}{T}\]となります.この式に\[\omega=\frac{2\pi}{T}\]を代入すると,\[V=r\omega\]となります.
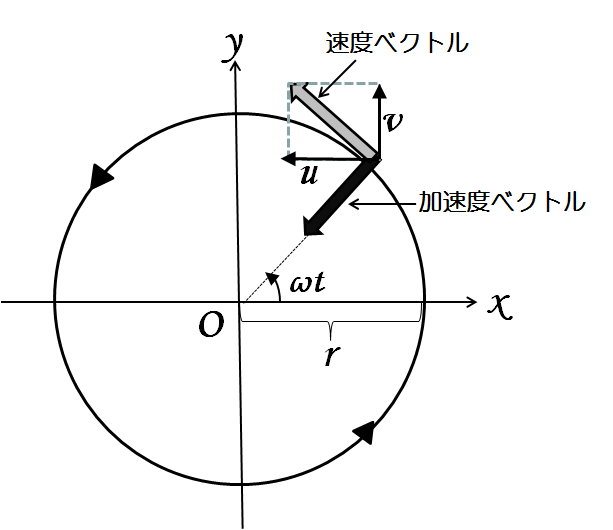
いま,図で点 $P$ に物体があるとします.そうすると,$x$ 方向の速度を $u$,$y$ 方向の速度を $v$ とおくと,\[\begin{align}u&=-r\omega\sin\omega t\\v&=r\omega\cos\omega t\end{align}\]となります.
次に$x$ 方向の加速度,$y$ 方向の加速度を求めます.$u,v$ を $sin$ 関数,$cos$ 関数の微分(⇒*)を用いて微分すると,\[\begin{align}u'&=-r\omega^{2}\cos\omega t\\v'&=-r\omega^{2}\sin\omega t\end{align}\]となります.
つまり,加速度ベクトルの大きさは,\[r\omega^{2}\]となるので,\[V=r\omega\]を代入すると,結局のところ加速度ベクトルは,\[\frac{V^{2}}{r}\]となります.この加速度ベクトルは円運動の中心に向いて,求心加速度(centripetal acceleration)といいます.
Mathematics is the language with which God has written the universe.